ブログ
2020年 9月 1日 物理のディメンション(次元)について

こんにちは。1年担任助手の菊地原です。
たびたびすみません。今回は力学のディメンション(次元)について話していきたいと思います。お付き合い下さい、、、

そもそも、物理の式が何で足し算、引き算出来ているか分かりますか?
それは、ディメンション(次元)が一緒だからです。速さ(m/s)と力の大きさ(N)を足し算しても何も求まらないよねって感じです。
じゃあこのディメンションを意識したら、何かいいことはあるの??と思ったそこの君!!あるに決まっているでしょう。
メリット1つ目はディメンションを知っていれば死んだと思った暗記問題に一筋の光が
差します。張力をS(N)、1m当たりの密度をp(kg/m)である弦を伝わる波の速度は
いくつですか。という問題があったとします。覚えている人は一瞬で答えを出せるかも
しれませんが、覚えてなかった場合は詰んだ、、、、と思うかもしれません。ですがここ
で、運動方程式(EOM)を思い出してください。F=maですね。これをディメンション解
析をすると、F(N)=m(kg)×a(m/s×s)となっています。つまり、ディメンションにつ
いて考えるとNは(kg×m)/(s×s)になっています。これを考慮してSとpを使って速
度v(m/s)になる形を考えると、v=(S/p)^(1/2)となるような気がします。実際これ
が答えです。絶対に合ってるとは確信は持てないけど、可能性がほぼ0だったところ
から比べると大分よくなったと思います。
メリット2つ目は検算に使えるということです。実際、このメリットが大半を占めていま
す。めっちゃ複雑な計算問題の答えが違ったらめっちゃ萎えませんか?そんな時この
ディメンションの考え方があれば無次元量のようなスカラーによるミス以外は消えま
す。これは入試の最終段階で大きく効いてきます。
是非使ってみてください!!!!下に参考程度に載せておきますね。
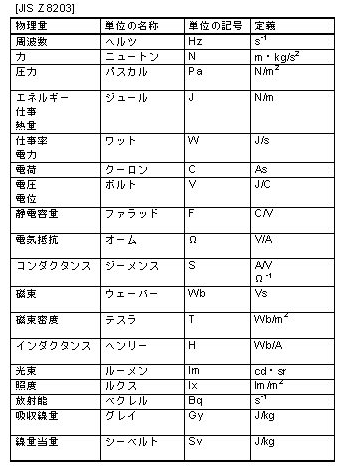
ちなみに、θは無次元量です。つまり、角運動量ωのディメンションは(無次元)/sです。気を付けてくださいね、、、、、
担任助手1年菊地原崚














